C++ 模板和模板偏特化

这是一个模板，在我刚刚看见它的时候。我觉得好像我什么都没看懂。

但是，过了不到两个小时，我就突然好像懂了什么，然后还能自己写一些代码。

在开始之前，得讲一下关于函数重载。

函数重载：

void print(int i) {
    cout << "Print int: " << i << endl;
}

void print(double f) {
    cout << "Print float: " << f << endl;
}

void print(char* c) {
    cout << "Print char: " << c << endl;
}

它在调用的时候，会根据输入的参数类型，自动选择调用哪一个函数。你自定义一个函数支持不同类型的参数列表，并且可以根据参数列表做出不一样的响应。

但是，它同样也带来了非常多的重复性代码。

模板的引入首先就解决了这个问题。

模板：

template <typename InT>

void print(InT i) {
    cout << "Print: " << i << endl;
}

这样一个模板会接受任意类型的参数，然后把它打印出来。

所以模板的使用同样潜在问题，需要约束输入参数，并且给出异常和提示支持的类型。

模板偏特化：

当模板写完之后，我们发现实际上，存在某些情况不能被我们的模板所支持。

现在再看我们最初提出的那个模板：

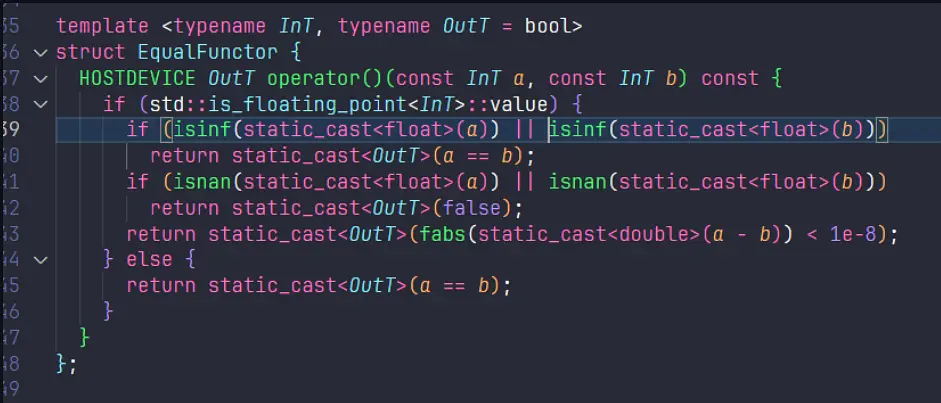
template <typename InT, typename OutT = bool>
struct EqualFunctor {
  HOSTDEVICE OutT operator()(const InT a, const InT b) const {
    if (std::is_floating_point<InT>::value) {
      if (isinf(static_cast<float>(a)) || isinf(static_cast<float>(b)))
        return static_cast<OutT>(a == b);
      if (isnan(static_cast<float>(a)) || isnan(static_cast<float>(b)))
        return static_cast<OutT>(false);
      return static_cast<OutT>(fabs(static_cast<double>(a - b)) < 1e-8);
    } else {
      return static_cast<OutT>(a == b);
    }
  }
};

它做了什么事情：

检查输入 a、b 是否都是浮点数，如果不是，直接返回 a == b
如果是浮点数，那么会存在一个精度问题，需要考虑边界(无穷大小和 0)
如果是无穷大或者无穷小，直接返回 a == b
如果是 NaN，直接返回 false
如果是浮点数，返回 fabs(a - b) < 1e-8 ，只要两者相差 <1e-8，那么认为这两个相等。这个是 float32 的最小精度。

但是，这个模板只考虑了实数范围的，它直接把 a 和 b 进行了比较。

如果是复数，我们需要考虑实部和虚部，并且分别比较。

也就是a.real，a.imag，b.real，b.imag。

这个时候，我们就需要对模板进行偏特化。

template <typename OutT>
struct EqualFunctor<phi::dtype::complex<float>, OutT> {
  HOSTDEVICE OutT operator()(const phi::dtype::complex<float>& a,
                             const phi::dtype::complex<float>& b) const {
    if (isinf(a.real) || isinf(a.imag) || isinf(b.real) || isinf(b.imag)) {
      return a == b;
    }
    if (isnan(a.real) || isnan(a.imag) || isnan(b.real) || isnan(b.imag)) {
      return false;
    }
    float epsilon = 1e-8f;
    return std::abs(a.real - b.real) < epsilon &&
           std::abs(a.imag - b.imag) < epsilon;
  }
};

template <typename OutT>
struct EqualFunctor<phi::dtype::complex<double>, OutT> {
  HOSTDEVICE OutT operator()(const phi::dtype::complex<double>& a,
                             const phi::dtype::complex<double>& b) const {
    if (isinf(a.real) || isinf(a.imag) || isinf(b.real) || isinf(b.imag)) {
      return a == b;
    }
    if (isnan(a.real) || isnan(a.imag) || isnan(b.real) || isnan(b.imag)) {
      return false;
    }
    double epsilon = 1e-8;
    return std::abs(a.real - b.real) < epsilon &&
           std::abs(a.imag - b.imag) < epsilon;
  }
};

我们保持模板名称不变，outT 也不变，但是我们对输入参数进行了偏特化。

这就是模板的变态之处了，它甚至支持部分参数的特化。

我们把模板的输入参数指定为phi::dtype::complex<float>和phi::dtype::complex<double>，然后在里面定义了对复数的处理逻辑。

而且还有更变态的。

我们发现对于复数的处理是完全一致的，但是复数有两个类型。

我们甚至还可以这样：

template <typename InT, typename OutT>
struct EqualFunctor<phi::dtype::complex<InT>, OutT> {
  HOSTDEVICE OutT operator()(const phi::dtype::complex<InT>& a,
                             const phi::dtype::complex<InT>& b) const {
    if (isinf(a.real) || isinf(a.imag) || isinf(b.real) || isinf(b.imag)) {
      return a == b;
    }
    if (isnan(a.real) || isnan(a.imag) || isnan(b.real) || isnan(b.imag)) {
      return false;
    }
    InT epsilon = 1e-8;
    return std::abs(a.real - b.real) < epsilon &&
           std::abs(a.imag - b.imag) < epsilon;
  }
};

我们只是把InT局部地去匹配float和double，这样子我们的模板就从两个变成了一个。

可以说，CPP 为了少写点代码真的是无所不用。

而当我看懂了模板，我发现 CPP 我就看懂了一大半。